コンプリート! 三角形の��度の和 325411-三角形の角度の和 何年生
好きな言葉は「全単射」。どうもこんにちは、ジャムです。 3日間ブログを更新していませんでしたね、すみません。 突然ですが皆さん、三角形の内角の和、何度か分かりますか? そりゃあみなさん、当たり前ですよね。 270°ですよねぇ!? という冗談はさておき、 みなさんが知って あとは「三角形の内角の和は \(180°\) 」「直線は \(180°\)」を使うと \(∠BAT=∠ACB\) となり、接弦定理を証明できました。 円の接線が接点を通る直径と垂直になる理由3.角度abc、角度bca、角度cabは全て90度である。 の理由によって 図形abcは間違いなく 直線の辺を3つ持つ三角形であり、 かつ内角の和が270度となります。 さらに最初の命題に戻りますが「内角の和が270度の正三角形」 についてはもうちょっと条件を追加して
多角形とは 外角 内角の和 面積 対角線の公式と求め方 受験辞典
三角形の角度の和 何年生
三角形の角度の和 何年生- 今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ=となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質 三角形の外角は他の二角の和に等しいと説明するか、錯角を使って説明するか。 私が、平面図形と睨めっこする間に子供は興味も集中力も失います。 やっぱりこのあたりが素人だなと反省。 パパの時よりずっと勉強してるよ、凄いねと言っても無反応。



内角の和 算数用語集
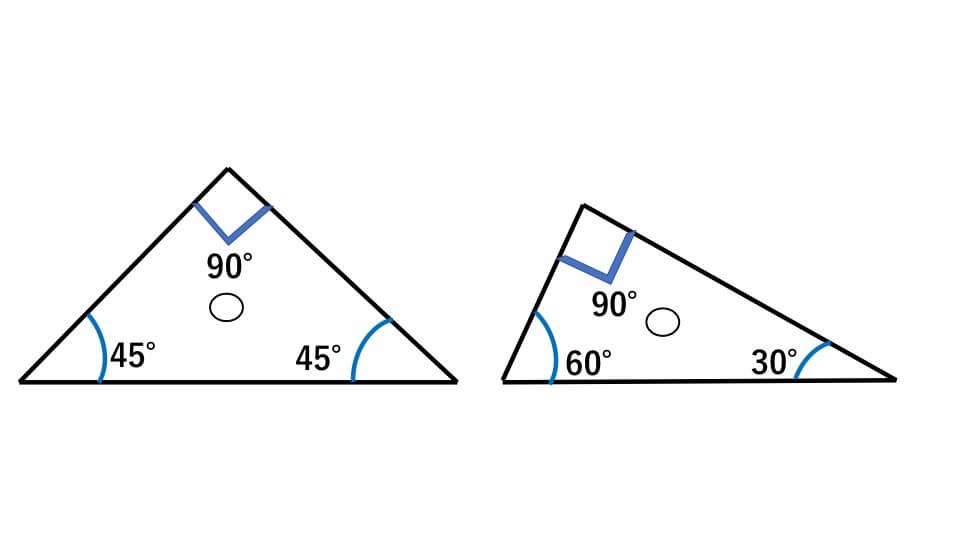
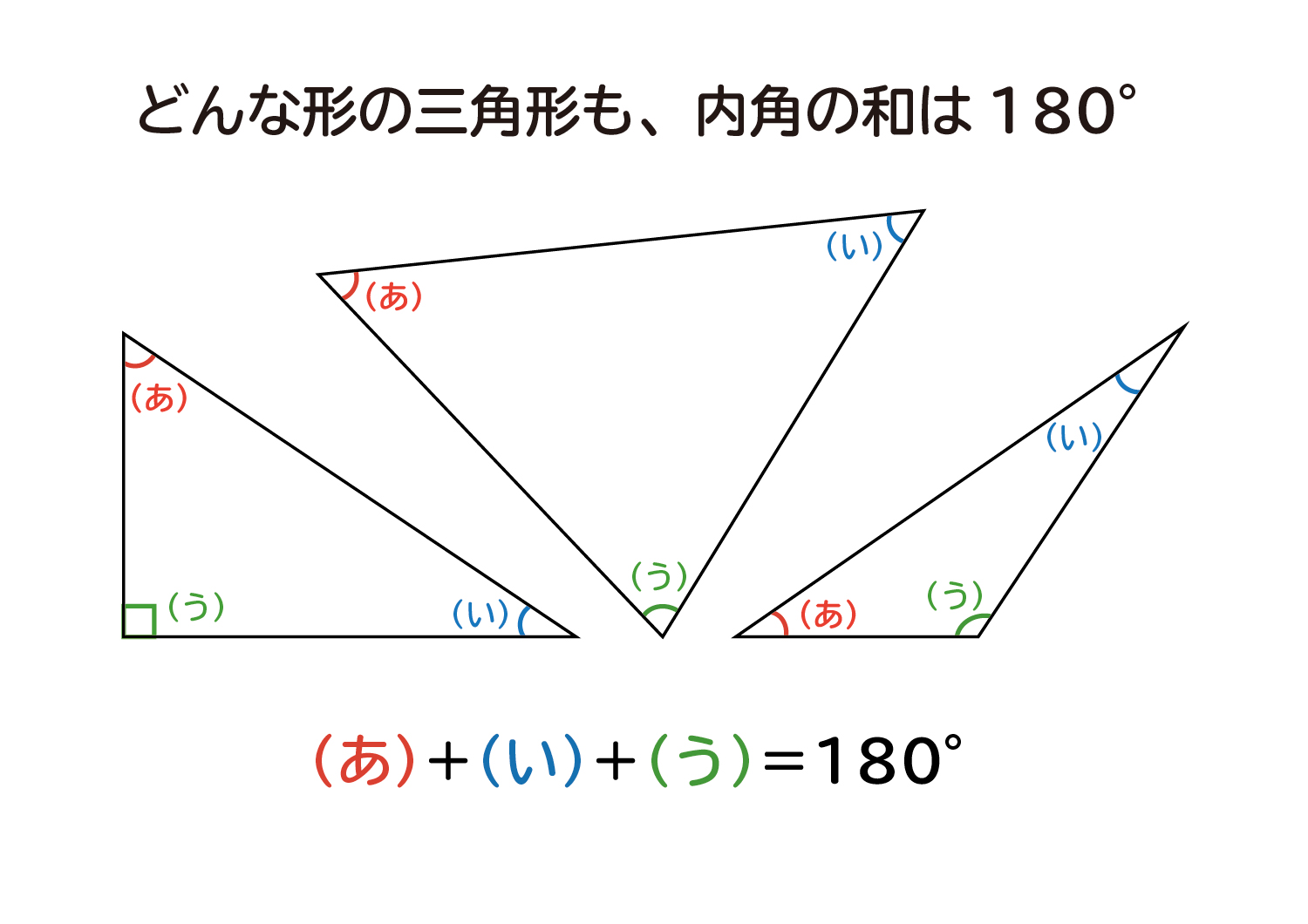
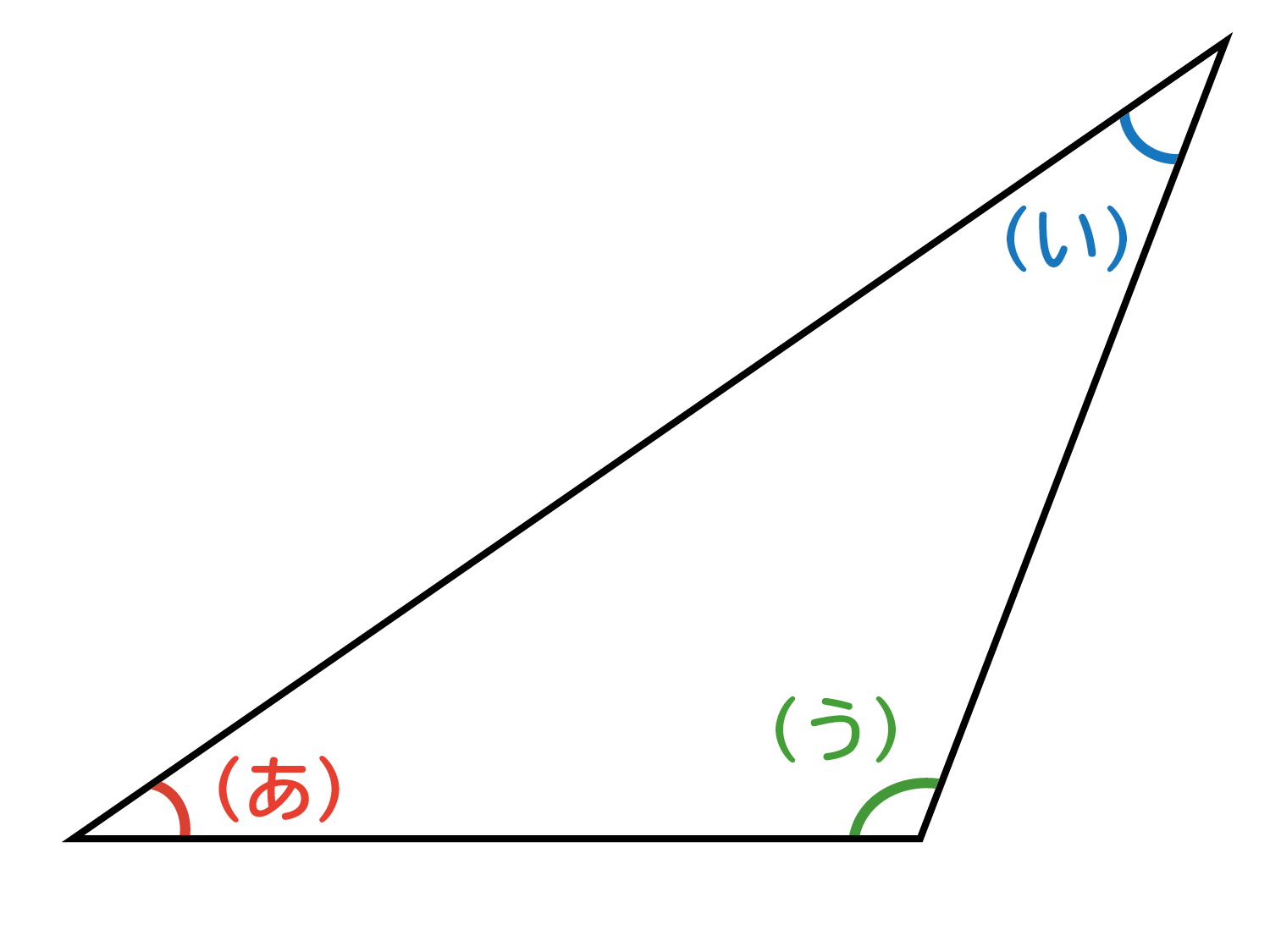
三角形の内角の和は常に \(180^\circ\) なので、最大角以外の \(2\) 角は必ず鋭角となる。 よって、三角形が鋭角三角形、直角三角形、鈍角三角形のどれであるかを調べるには、最大角 \(\mathrm{A}\) が鋭角、直角、鈍角のどれであるかを調べればよい。星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用して三角形の内角の和は この三角定規の内角の和は、60+90+30=180°です。 この三角定規の和は、90+45+45=180°です どちらの三角定規も、内角の和は180°です。 これは偶然でしょうか、 それとも、他の三角形も内角の和は180°になるのでしょうか。
球面上の三角形の内角の和 s = r 2 (a b c − π) s=r^2(abc\pi) s = r 2 (a b c − π) を証明できました。ここで,任意の三角形に対して面積 s > 0 s > 0 s > 0 なので a b c > π abc > \pi a b c > π が成立します! つまり, 球面上の三角形の内角の和は π \pi π より 三角形の角度を計算する方法 三角形には3つの角があります。もし3つが同じ角なら、それは全て 60度です。もし1つの角が 90度、つまりl字型をしていたら、それは直角三角形です。計算して角を求めることができるのです。こちらでは角度の計算について解説します。 (1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。
三角形の内角の和が180度なのは知っていますよね? その三角形が2個あります。 つまり、 三角形1と三角形2の内角の和の合計が 四角形の内角の和 になるということ。したがって 四角形の内角の和=360度 となるのです。三角形の内角と外角 三角形の内角の和は180°になる >>三角形の内角の和証明 三角形の1つの外角はそれと隣り合わない2つの内角の和に等しい a b x ∠x=∠a∠bである。 >> 説明 例 図で、∠xを求める。 x 34° 66° 三角形の内角の和は180°なので ∠x66°34°=180°・直角三角形(底辺と角度) 直角三角形の底辺と角度から、高さと斜辺と面積を計算します。 ・直角三角形(高さと斜辺) 直角三角形の高さと斜辺から、底辺と角度と面積を計算します。



内角と外角 中学受験算数 基本問題 どう解く 中学受験算数




タンジェントとは何か 中学生でも分かる三角関数の基礎
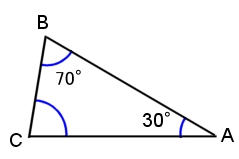
三角形の内角 三角形の3つの内角の和 → 必ず180°になる 問題 xの角度は??簡単だね?3つの内角を全て足し算すると180°だから、 40°65°∠x=180° ∠x=75° ・・・(答え) 三角形の外角 赤色の角度のことを、ぜんぶ 「外角」 と呼ぶよ!図形の角度 三角形の角度1 三角形の角度1 目標時間 名前 三角定規の3つの角度の和を求めましょう。 ① ② ア イ ウ イ ウ ° ° 正三角形の3つの角度の和を求めましょう。 ア イ ウ ° ア~エの角度を計算で求めましょう。 ① ② ° ° ア ° ° ③ ④ エ ° ° ° ア イ三角形の3つの角の大きさの和は,180°になる 三角形の内角の和は180°であることを 理解している。 数量や図形についての知識・理解 〔適用問題・ワークシート〕 計算で三角形の内角の大きさを求めるこ とができる。
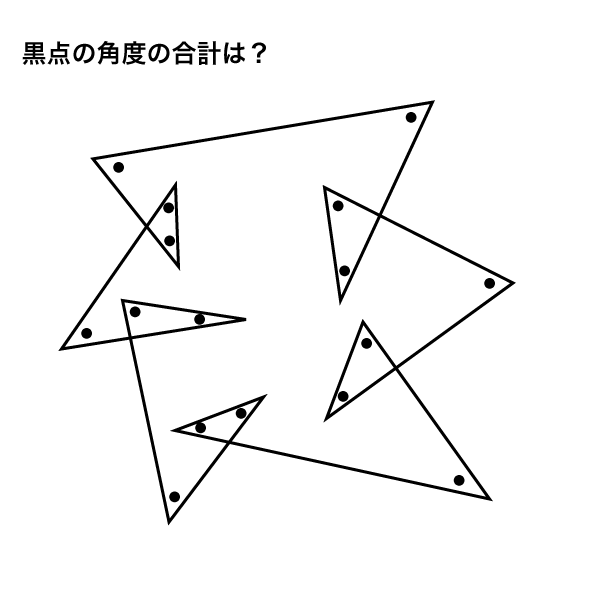



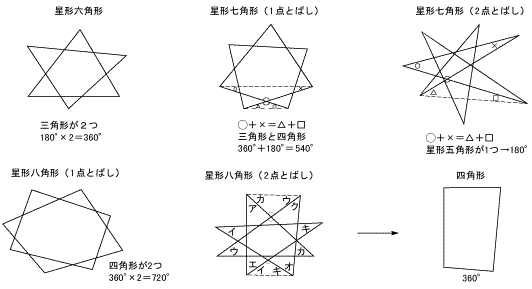
角度情報がない図形の合計の角度 星形多角形
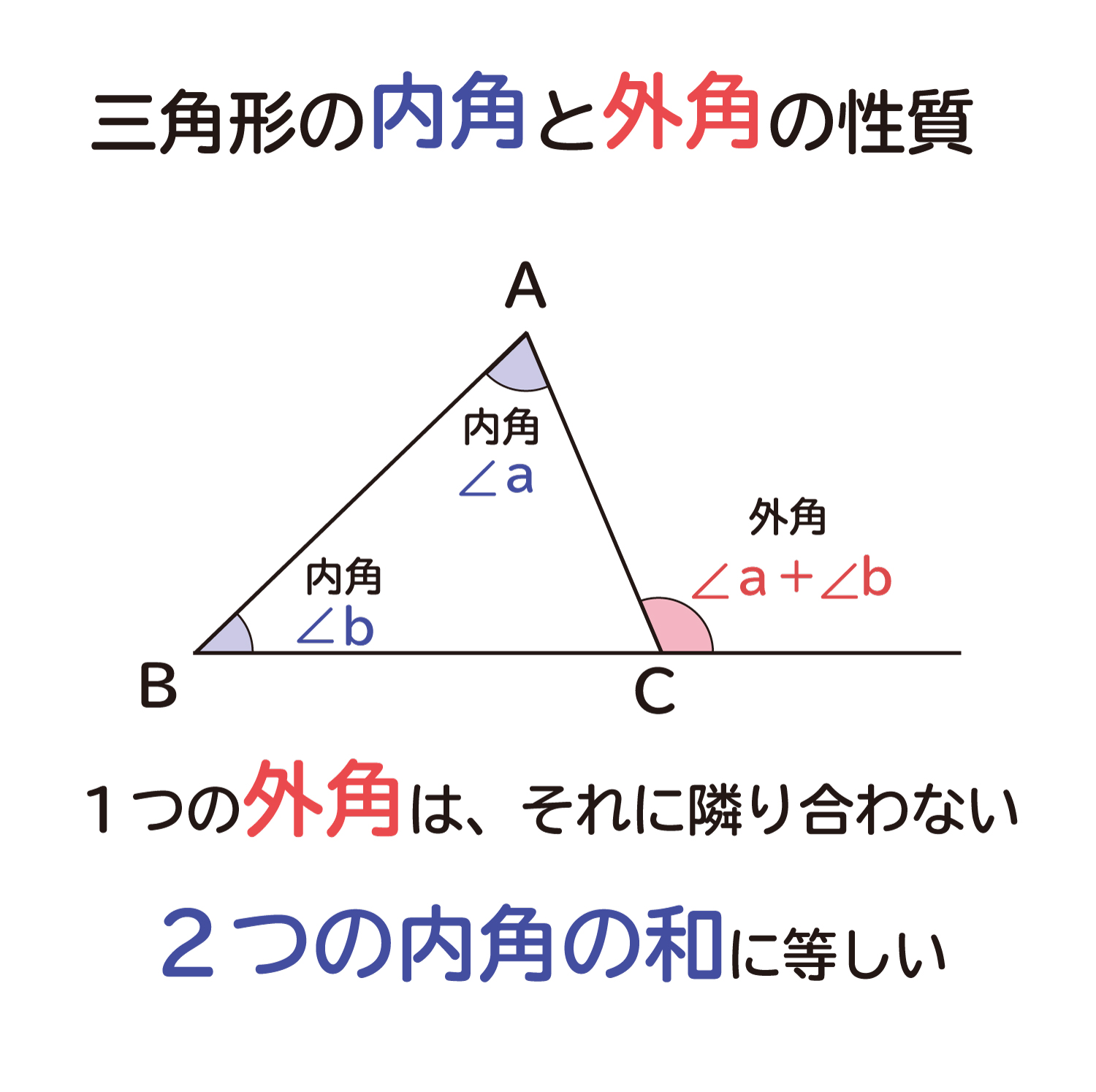



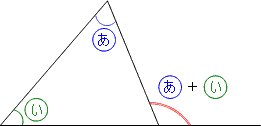
なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル
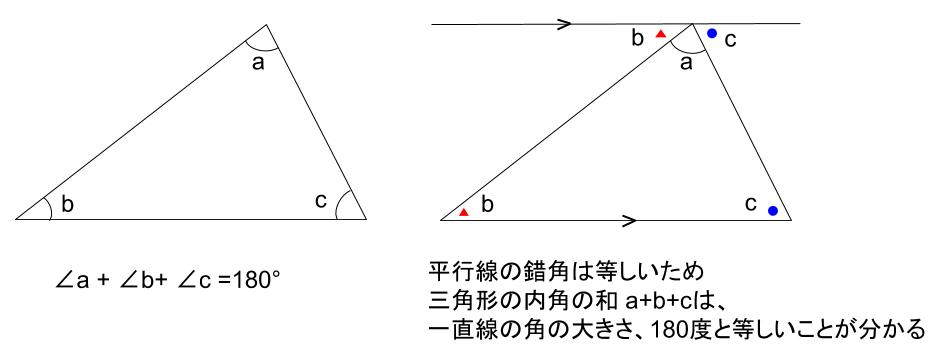
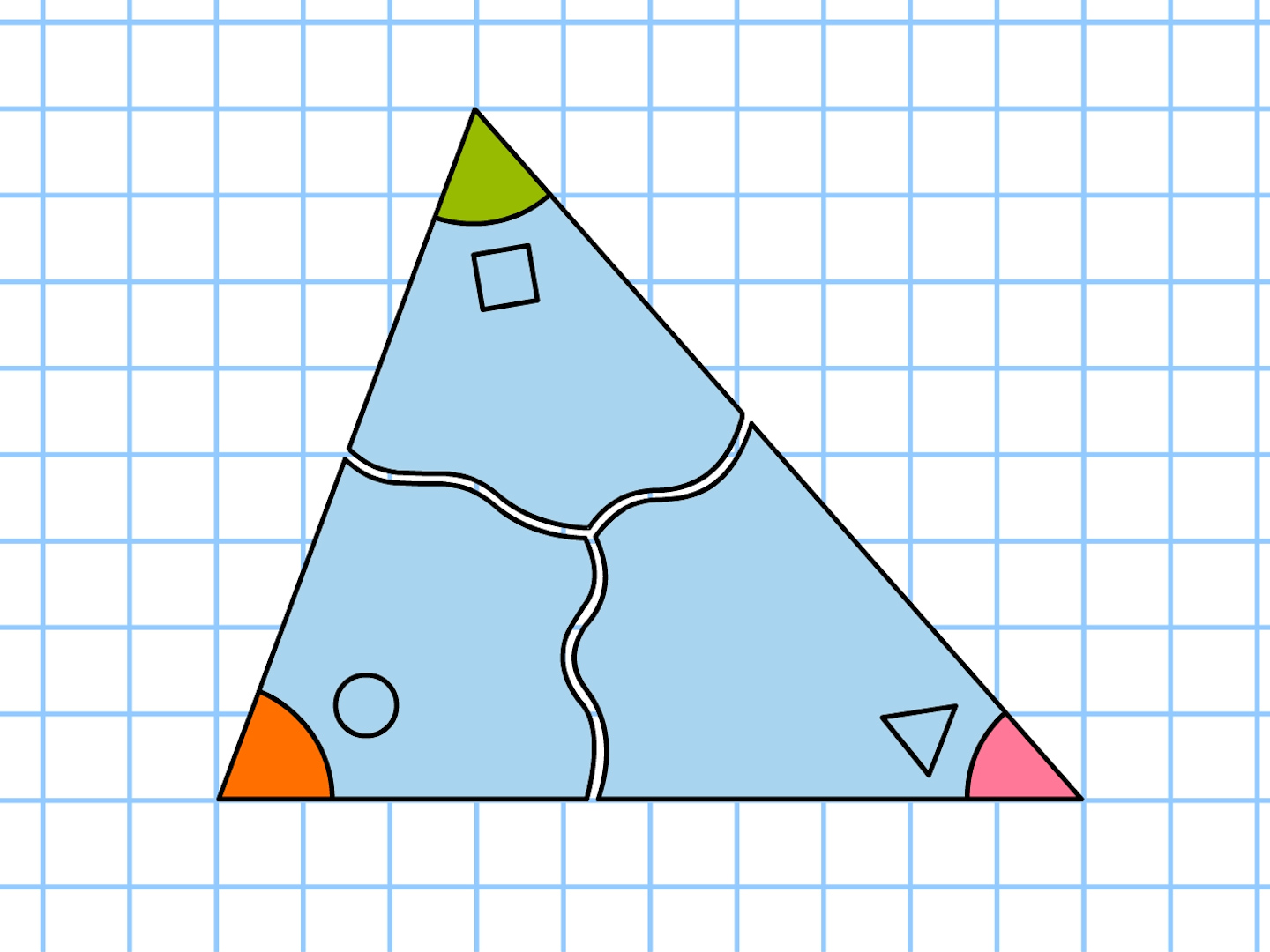
三角形の外角 三角形の外角は、これととなり合わない \(2\) つの内角の和と等しい。 また、三角形の外角は \(6\) 箇所あります。 いろいろな向きに対応できるように目を慣らしておきましょう。 角度の例題 例題1 下図の角 \(x\) の大きさを求めなさい。 解答三角形の3つの角をあわせると180°! これは、この三角形が特別な三角形だからできたことではありません。 どんなかたちの三角形でも、必ずこのように3つの角を集めて180°を作ることができるんです。 「三角形の内角の和」の視覚的導入 三角形の内角和 まず適当な3点をGeogebra上に定義する。 例えば2点A,Bをx軸上、残り1点CはXY平面状のどこか。 次にそれぞれ3点を直線で結んで三角形を完成させる。 角度を計測する関数angle (または角度計測ツール)を用いて三角形の内角をa1 = angle (B,A,C), a2



3
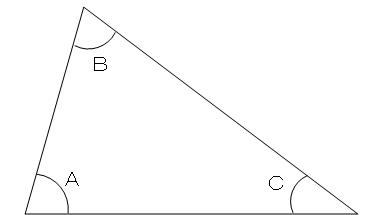



三角形の内角と外角の関係
こんにちは、ウチダです。 今日は、中学2年生で詳しく学ぶ 「三角形の内角の和」 について、それが180度である証明や、三角形の外角に関する公式・問題を解説していきます。 また、記事の後半では「内角の和が270度である三角形」についても考察し 「ドラゴン桜」みたいなNote街の「寺子屋」で伝えたい話 その5 前回の続き: 意外と手間取る人が多い「三角関数」について 重要ポイントを書きたいと思います 三角関数と言えば、サイン・コサイン・タンジェント 数1に三角比という単元がありますが、三角形の角度の世界 (=内角の 三角形の角度を求める問題です。ごく基本的な問題なので、確実に出来るようにしましょう。ポイント 三角形の内角の和は180度 内角と外角はどこか 三角形の1つの外角は、となりあっていない2つの内角の和に等しいこの3つのことを教科書などでしっかり確認してから問題に取り組んでく
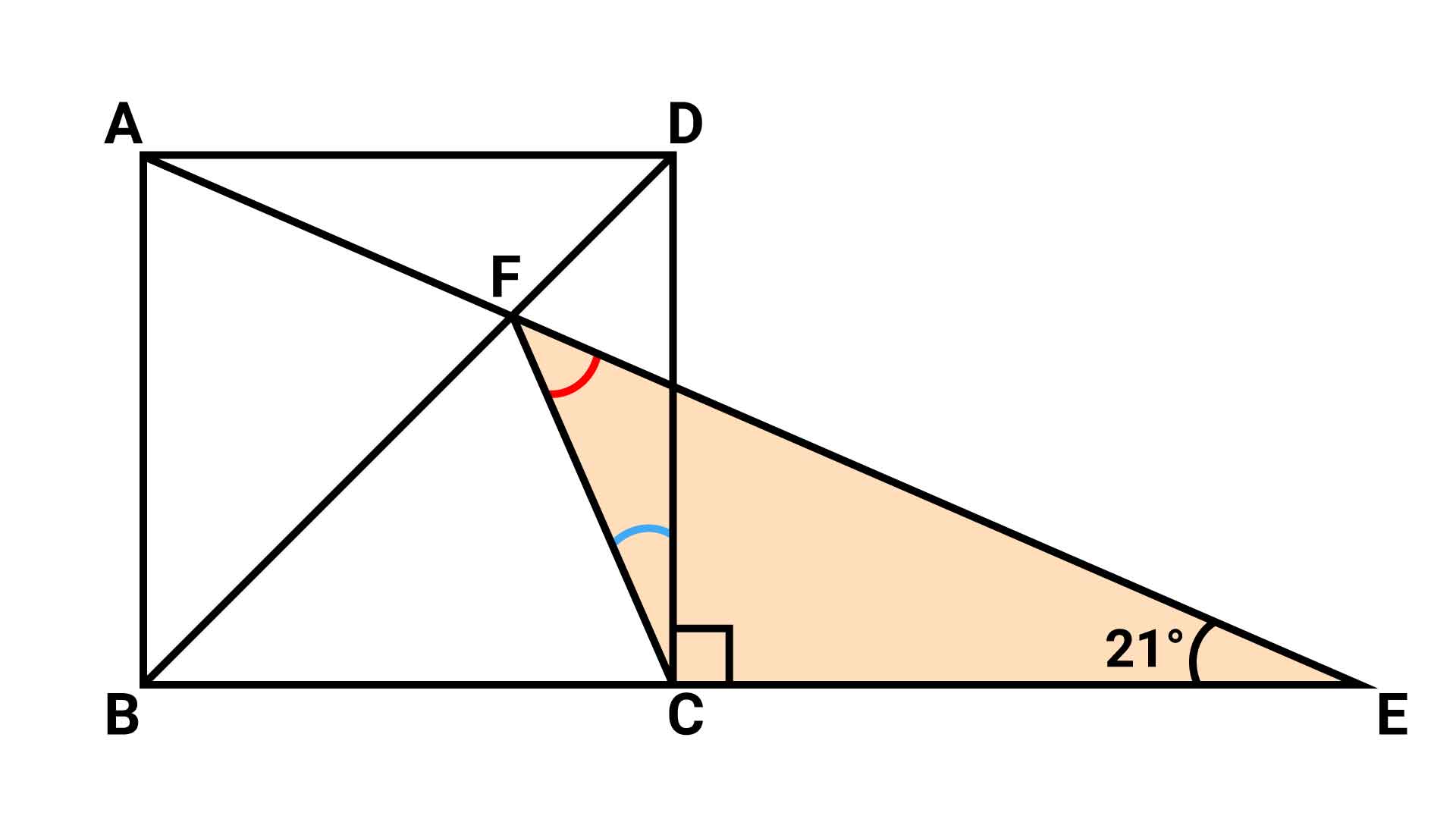



解けそうで解けない 小学5年生レベルの角度の問題に挑戦




数学 中2 48 三角形の内角と外角 基本編 Youtube
問題の印をつけた部分の和は三角形7つ分の内角の和-( の和+ の和) となり、180°×7-360°×2=540°となります。 内側に三角形タイプ 角の和 内側に三角形ができているタイプでは、補助線をひき、リボンの定理を使います。 例題4三角形の角の大きさの和 名前 日にち 月 日 小学5年生 (あ)の角度を求めましょう。 (1)三角形の3つの角の和は °です。 ( ) (2)正三角形の1つの角は °です。 ( ) (3)三角形の角の2つの大きさが°,33°のとき、のこりの1つの角のまた正三角形の場合、すべての角度が等しいです。三角形の内角の和は180°なので、正三角形ではすべての角度が60°です。 $180÷3=60$ 正三角形では角度が決まっています。 ・二等辺三角形 2つの辺の長さが等しい場合、その三角形を二等辺三角形といいます。



台形とは 定義や 台形の面積の公式をわかりやすく解説 受験辞典
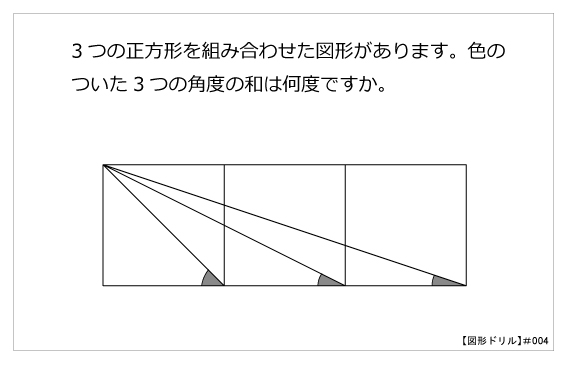



第4問 正方形の角度 図形ドリル 第4問 正方形の角度 算数星人のweb問題集 中学受験算数の問題に挑戦



三角形内角和是多少度 科学 科普 数理化科学




中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Qk2o5l4zzzb87m
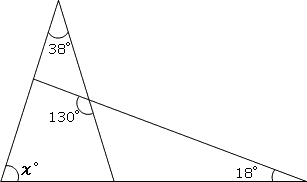



角度の求め方 算数の教え上手 学びの場 Com




06年 巣鴨中学校 算数 角度の和
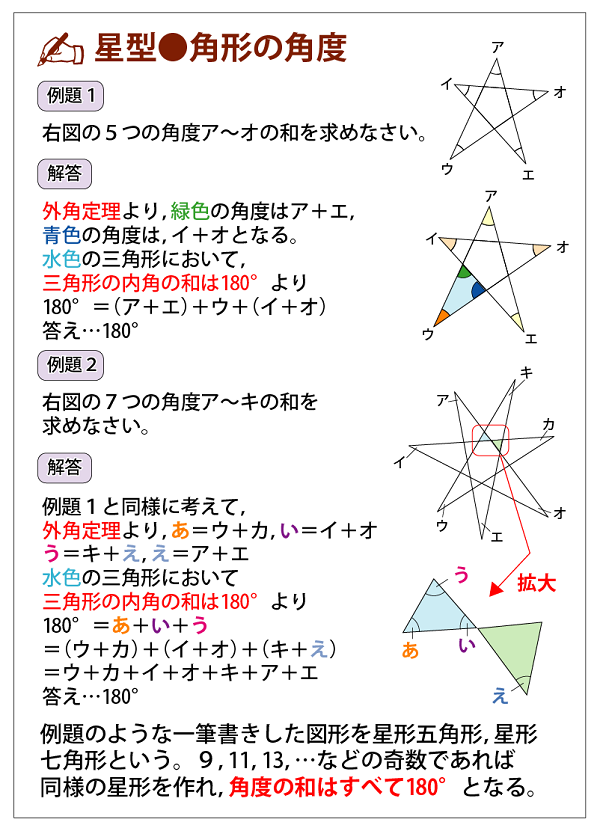



星型 角形の角度の問題 恋する中学受験 大学受験を見据えた中学受験




三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学




小5 算数 小5 31 三角形の角 Youtube




正三角形や二等辺三角形の内角 Youtube




三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
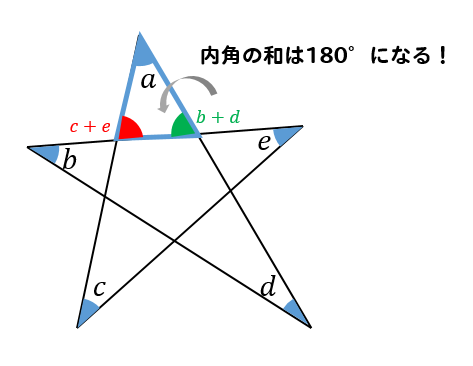



星形の角度 内角の和の求め方を問題解説 数スタ
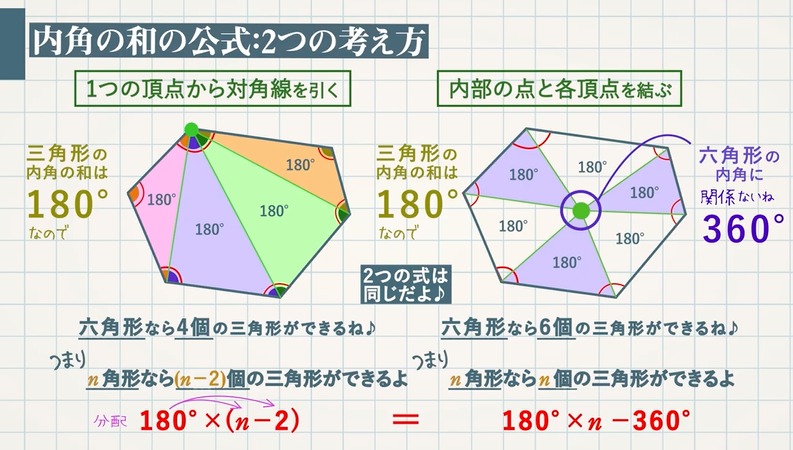



内角の和 180 N 2 外角の和 360 教遊者
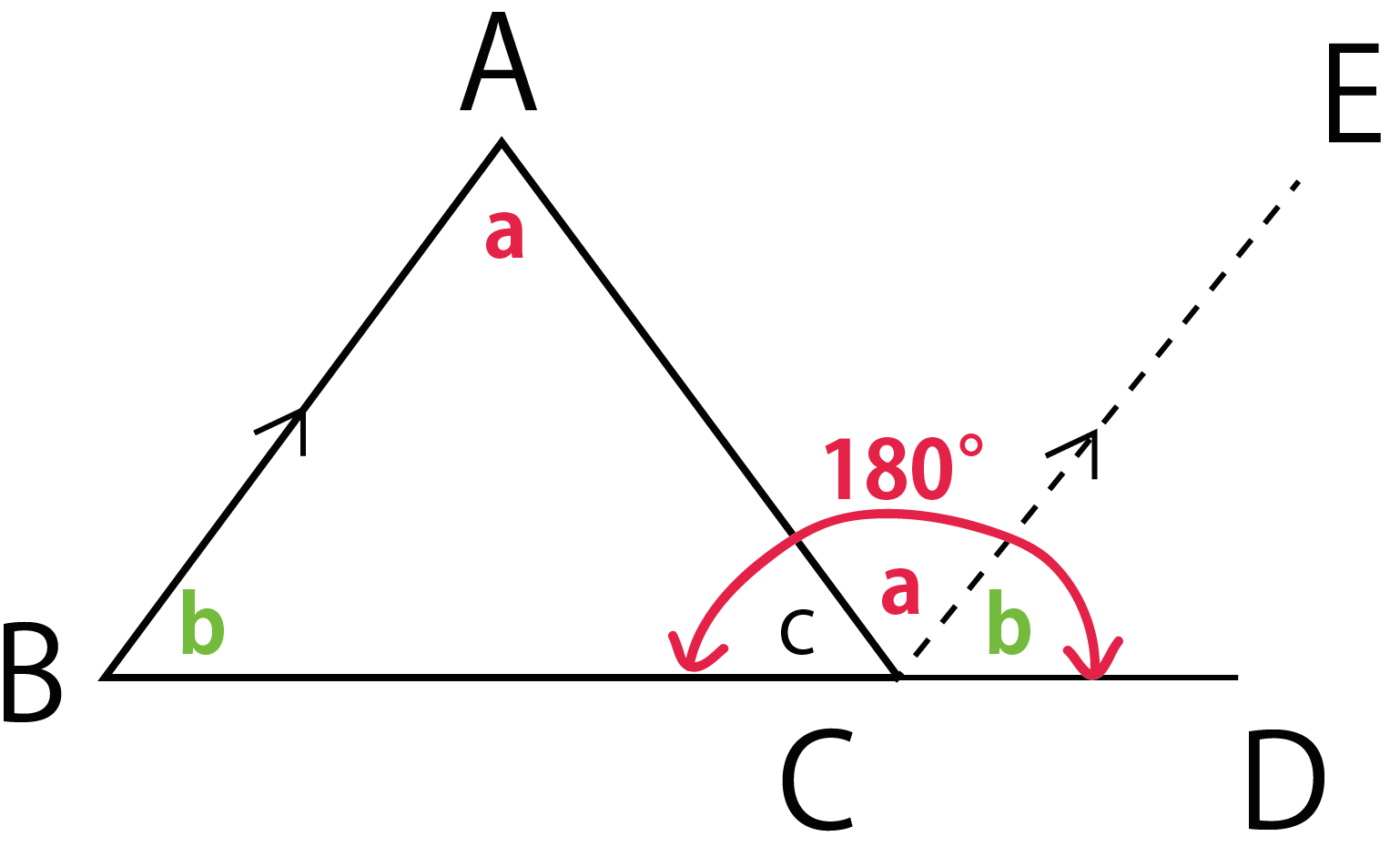



中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
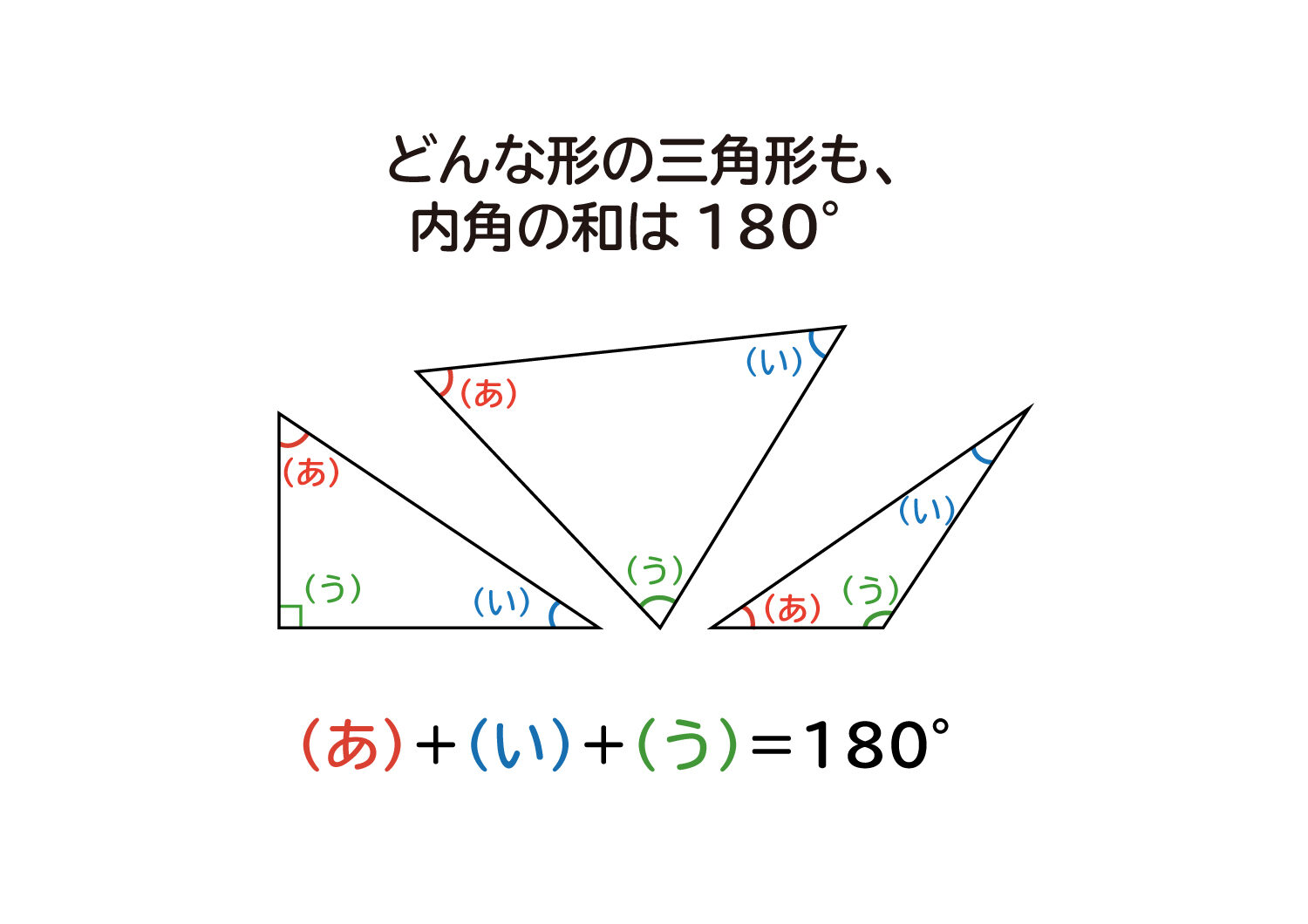



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル
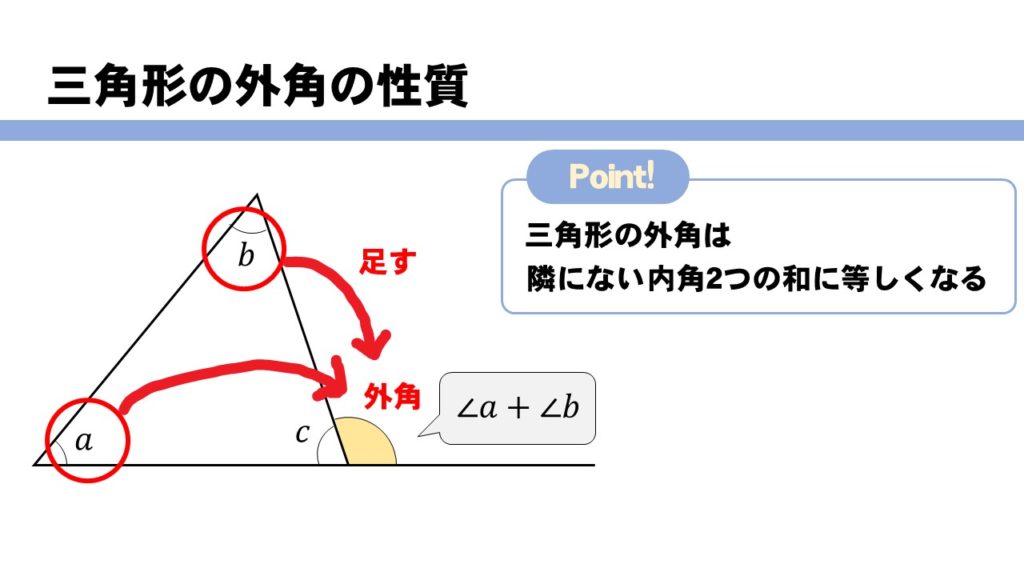



3分なるほど 三角形の内角 外角の性質について解説 数スタ




内角の和 180 N 2 外角の和 360 教遊者



3



内角の和が270 の正三角形




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
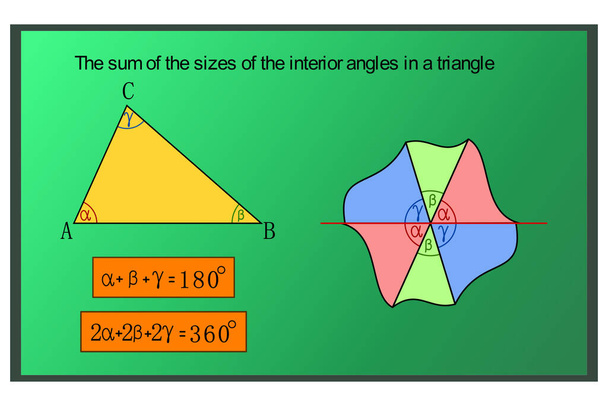



Straight Angleロイヤルティフリーのストックベクター




図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に



しょうちゃん 公式ブログ 三角形の内角の和は180度 Powered By Line




多角形の内角の和 算数の公式覚えてますか
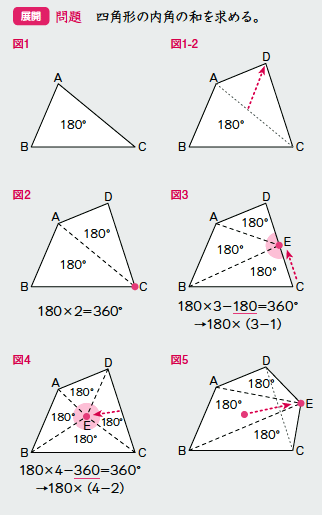



活用 の視点を取り入れた授業例 2 図形の性質 四角形の内角の和 5年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所




三角形の内角と外角の性質 教遊者
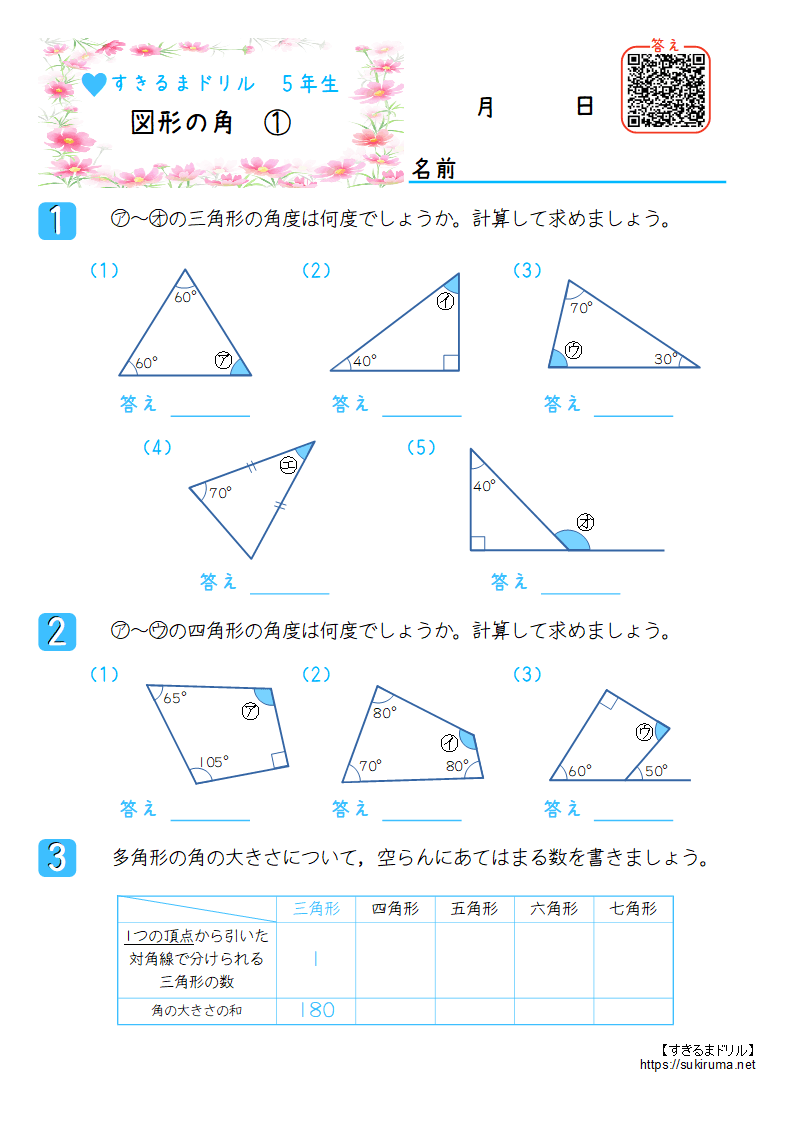



すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 幼児 小学生の無料学習プリント




3种方法来求三角形的第三个角




内角の和 算数用語集
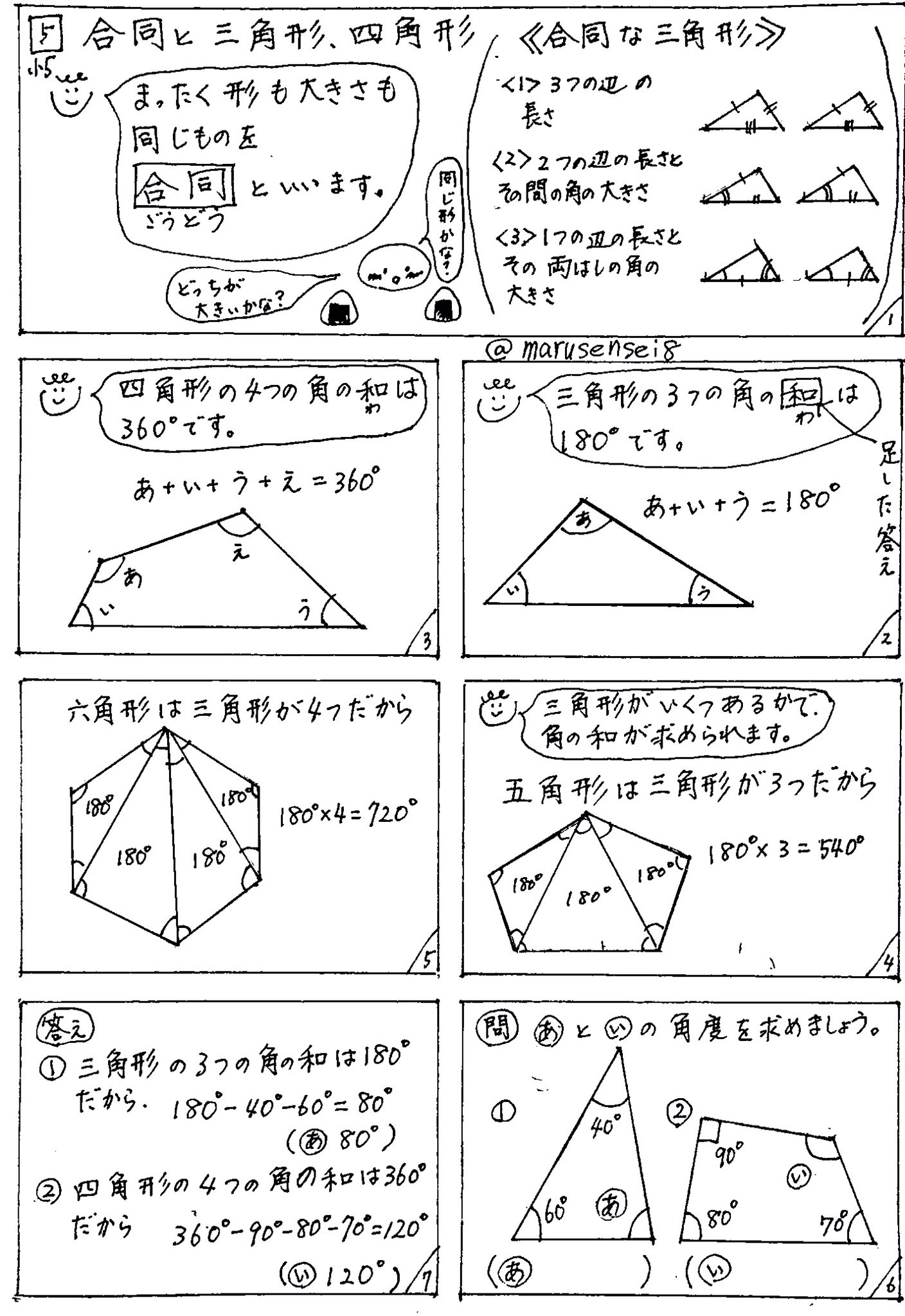



内角の和 Twitter Search Twitter
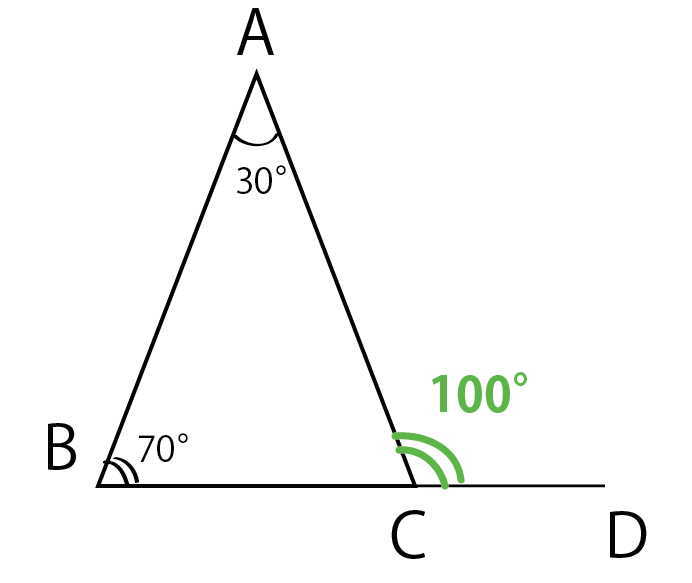



3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく




三角形の角度を求める問題 小学生 中学生の勉強
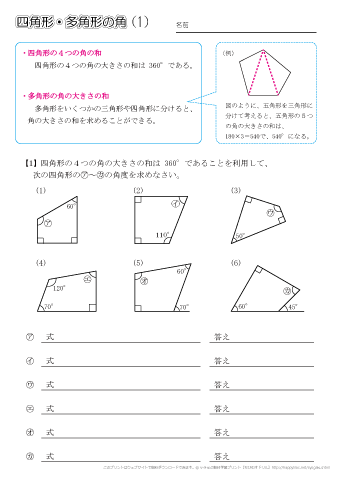



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
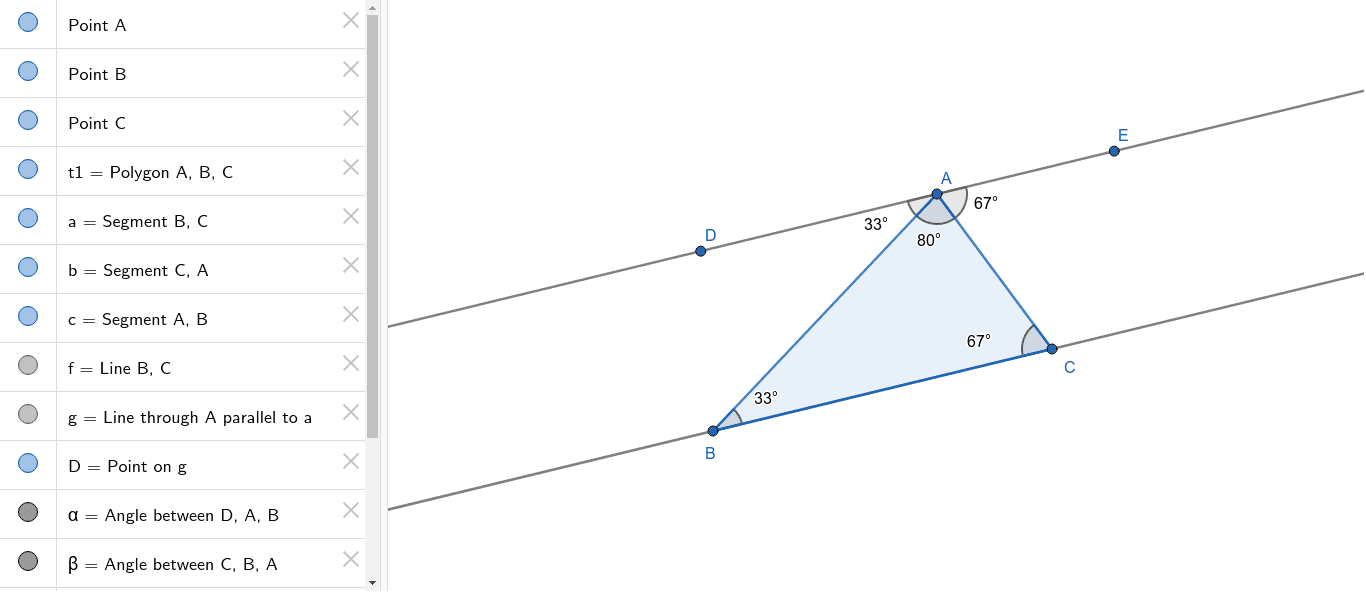



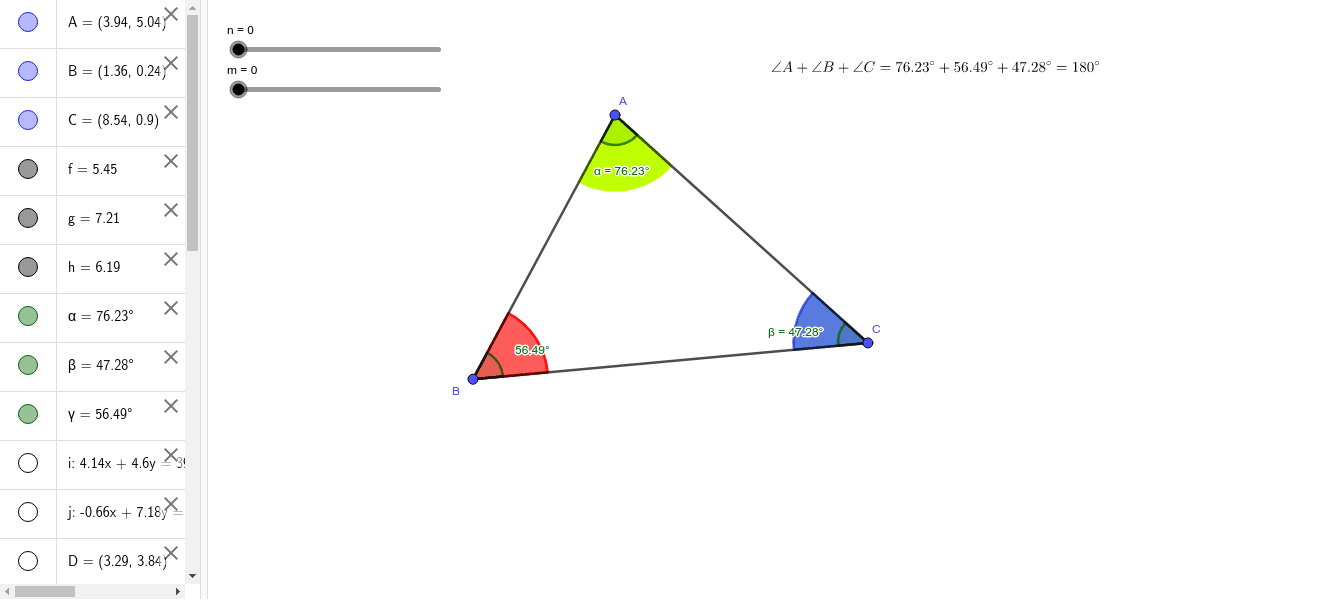
三角形の内角の和 Geogebra
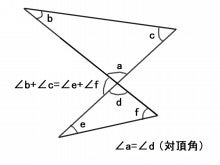



角度の求め方 数学が嫌いなんです




小5 算数科 字幕 三角形の内角の和 Youtube
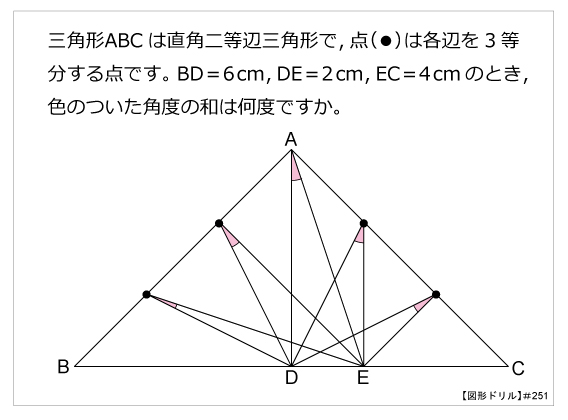



第251問 5つの角度の和 図形ドリル 第251問 5つの角度の和 算数星人のweb問題集 中学受験算数の問題に挑戦



Math 平行と合同 角の二等分線と角度 働きアリ




中2数学 ブーメラン型角度の求め方を解説 数スタ




さんすうをべんきょうしよう 三角形の内角の和が180度のやさしい証明 2
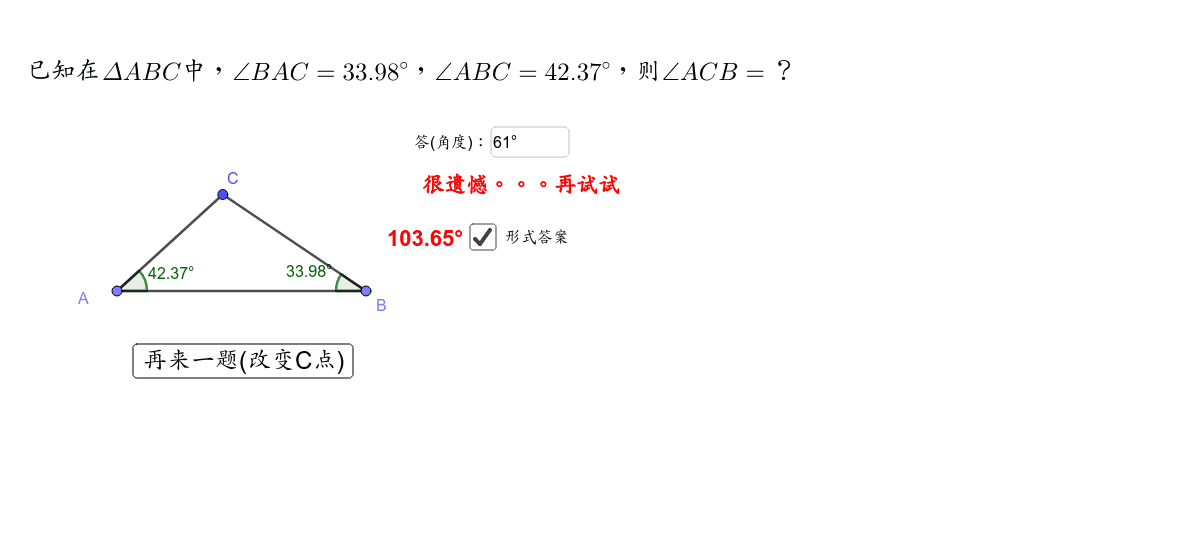



三角形内角和练习题课件 Geogebra
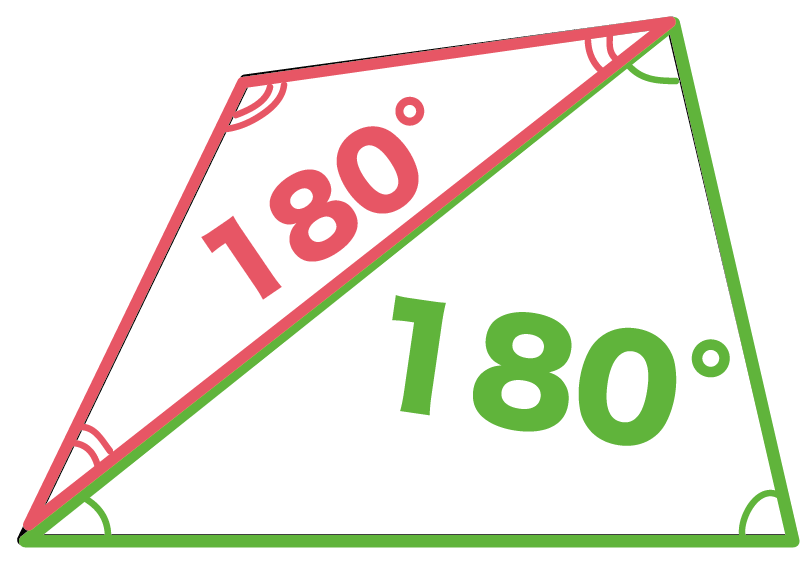



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく




三角形の内角の和
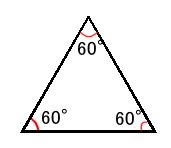



正三角形の内角の和
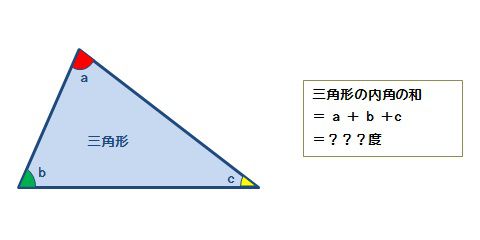



三角形の内角の和 算数の公式覚えてますか




多角形の内角の和 外角の和の公式 数学fun




三角形の角度 無料で使える中学学習プリント



図形の扉 三角形の外角の定理



中学数学 三角形の内角 外角 中学数学の無料オンライン学習サイトchu Su




中2数学 複雑な多角形 角の和 応用問題




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学受験 算数 角度 基礎からわかりやすくポイント解説 中学受験アンサー



5年 三角形のふしぎ 算数イメージ動画集 大日本図書



三角形内角和 Geogebra




内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学




多角形の内角の和の公式と外角の和を利用した角度の求め方
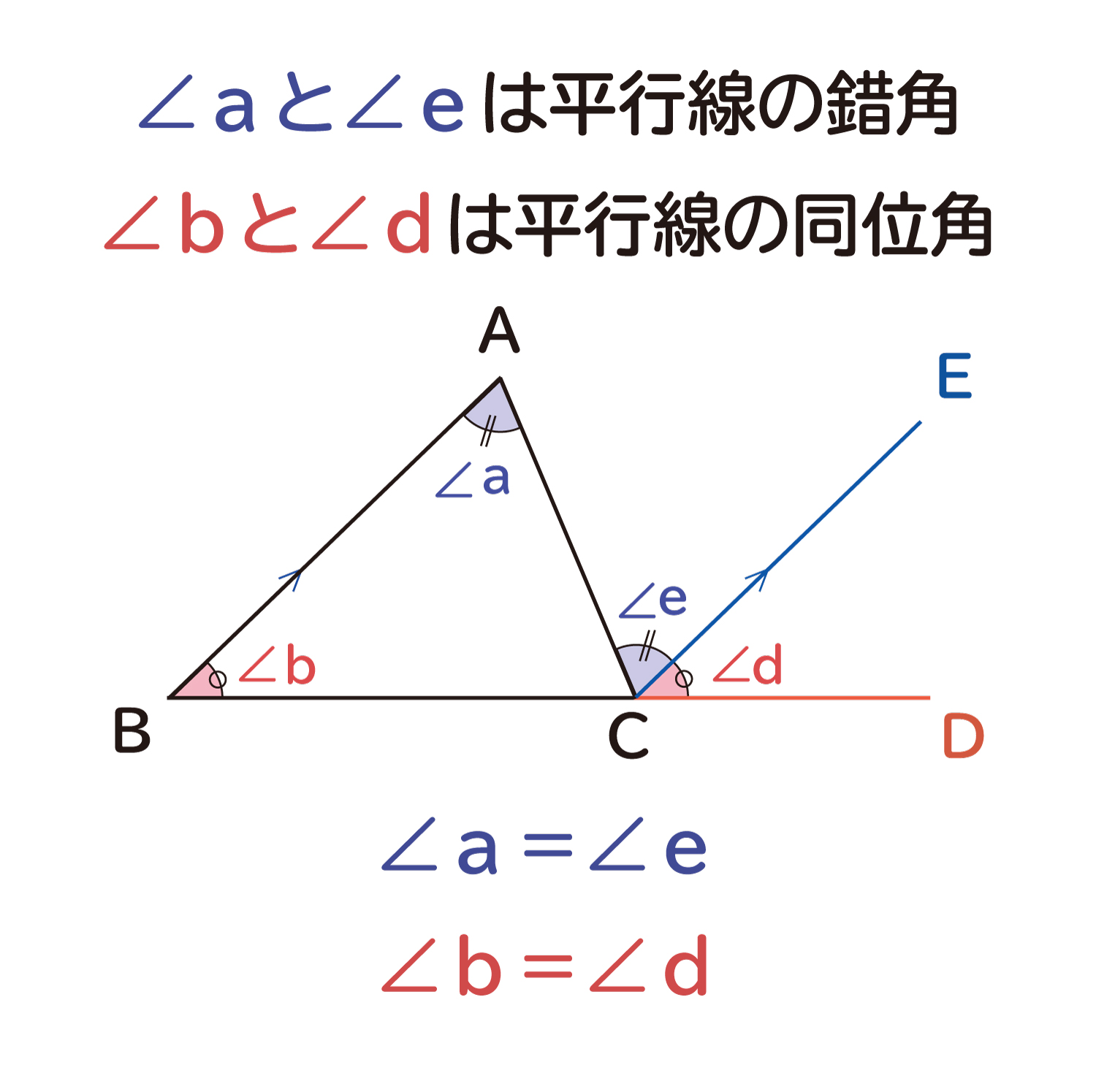



なぜ 三角形の1つの外角は それと隣り合わない2つの内角の和に等しい のか を説明します おかわりドリル
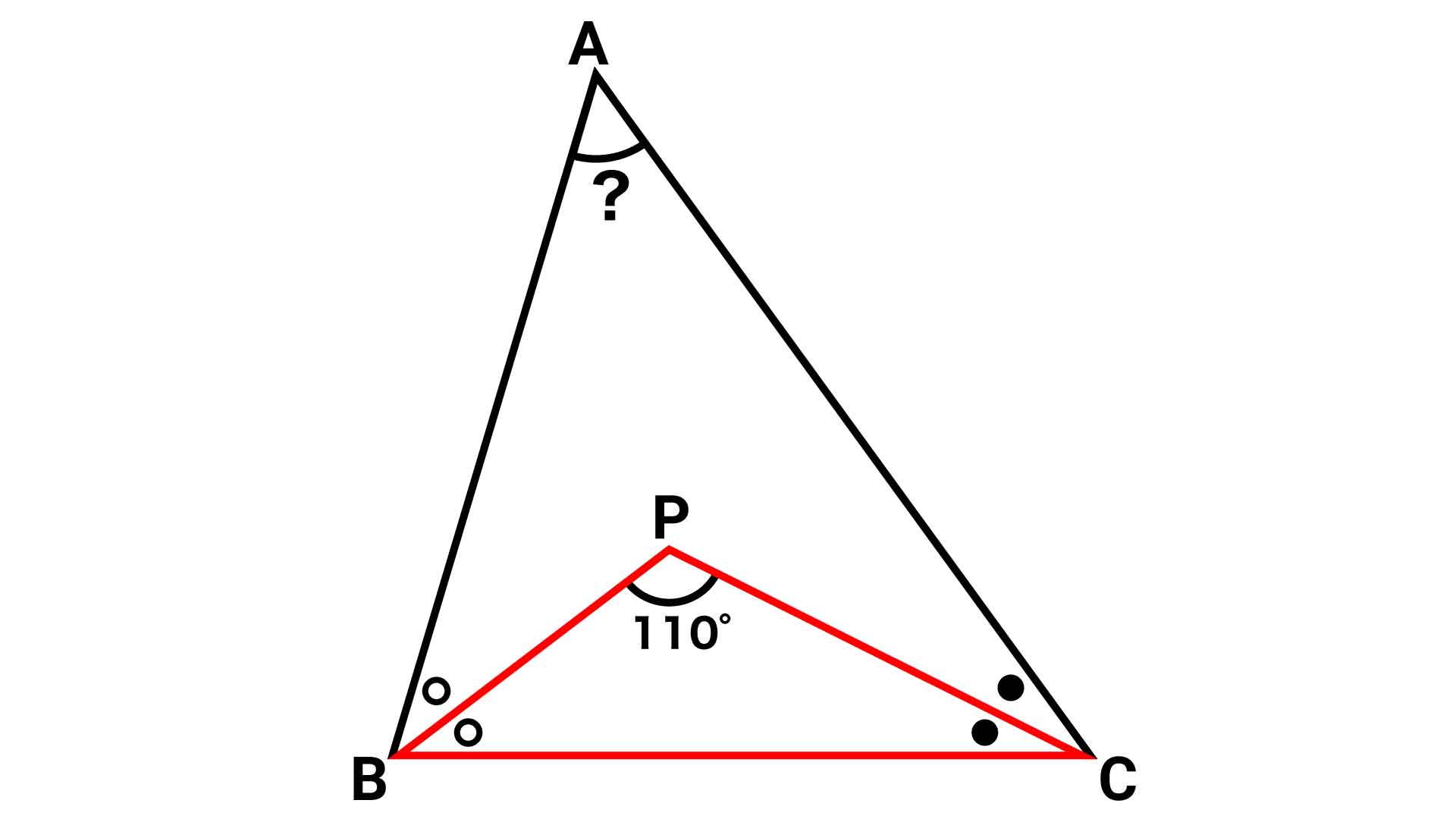



小学5年生で解ける 三角形の角度 の問題 あなたは解けますか




内角の和 算数用語集



角度の求め方 算数の教え上手 学びの場 Com




数学 中2 51 多角形の内角と外角の和 基本編 Youtube
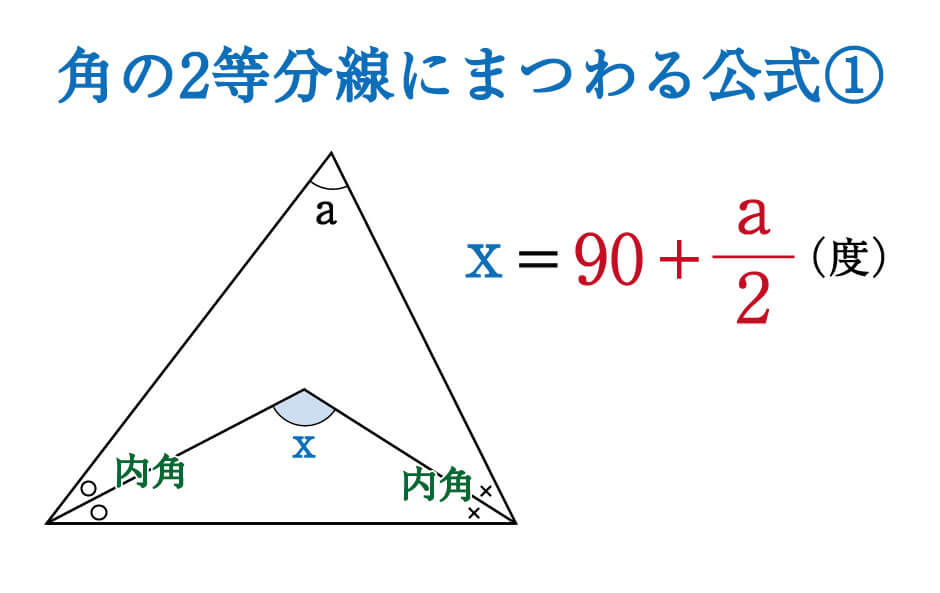



数学 角の二等分線にまつわる絶対に覚えておきたい公式 受験の秒殺テク 8 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
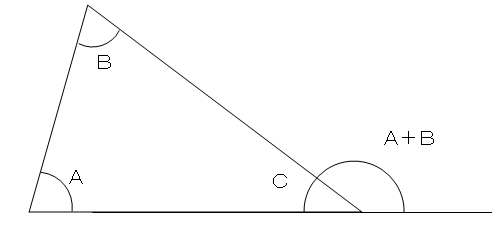



三角形の内角と外角の関係



内角の和が180 にならない三角形は存在しえますか Quora



証明 三角形の内角の和は180度 ちかでぃくの




課題学習の指導 数学



直角三角形の解法 1
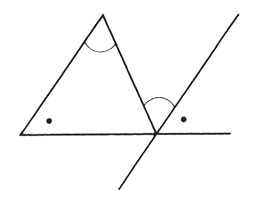



内角の和 算数用語集




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく
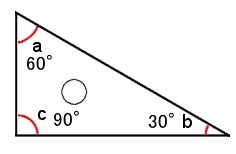



三角定規 さんかくじょうぎ の角度2



多角形とは 外角 内角の和 面積 対角線の公式と求め方 受験辞典



ア キの7つの角度の和は 開智未来中学 2012年 中学受験ー算数解き方ポータル
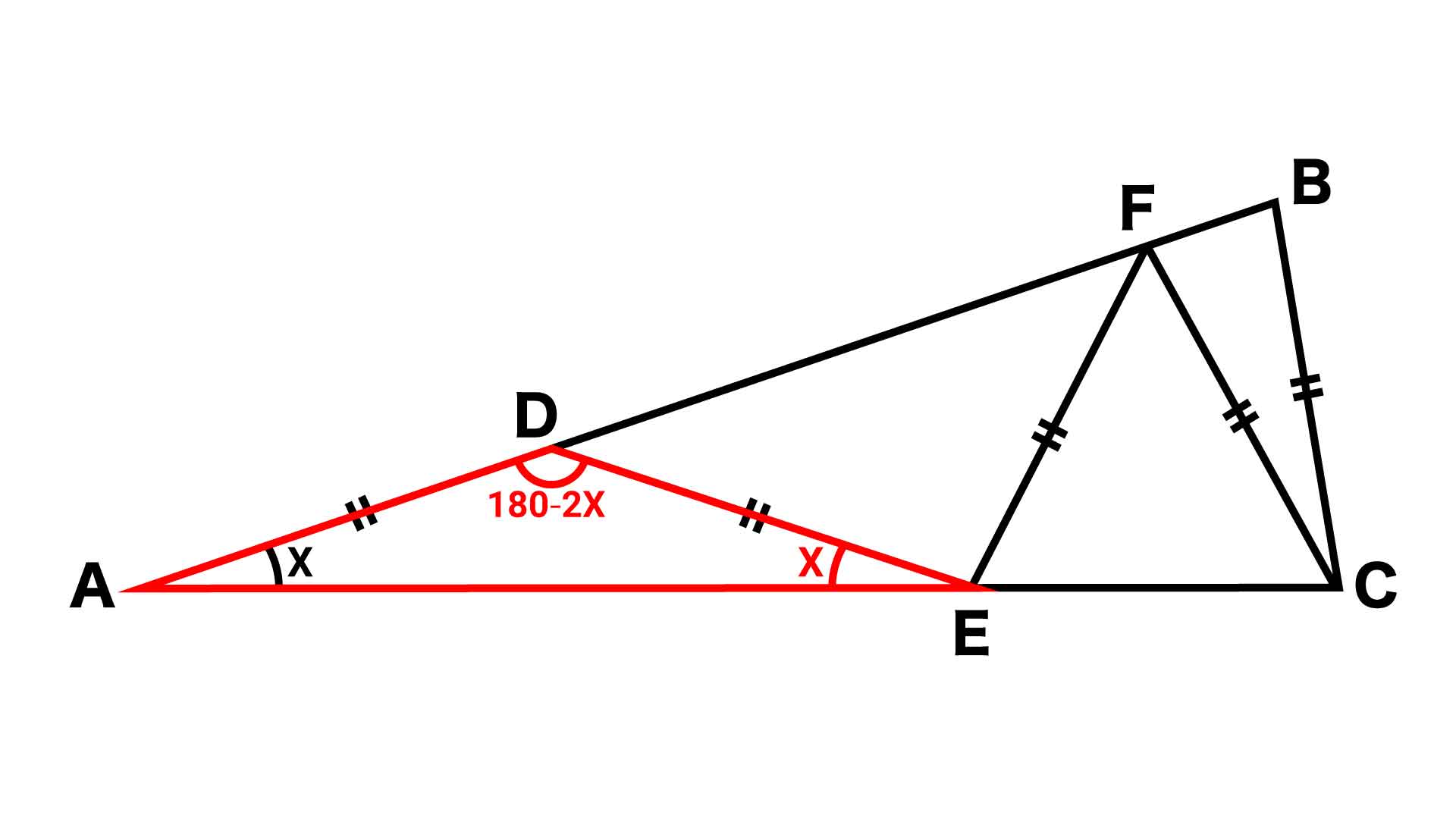



中学受験レベル 小学5年生で解ける 二等辺三角形 の問題に挑戦




三角形の内角の和を帰納的 演繹的に求める方法 算数を究める



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル



角度の求め方 算数の教え上手 学びの場 Com




さんすうをべんきょうしよう 三角形の内角の和は180度 3




多角形の内角の和 は何度なのか を説明します おかわりドリル



1



なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル




内角の和 180 N 2 外角の和 360 教遊者



三角形の作る角度1 3




Geogebraによる幾何学2 三角形の内角和 つれづれなる備忘録
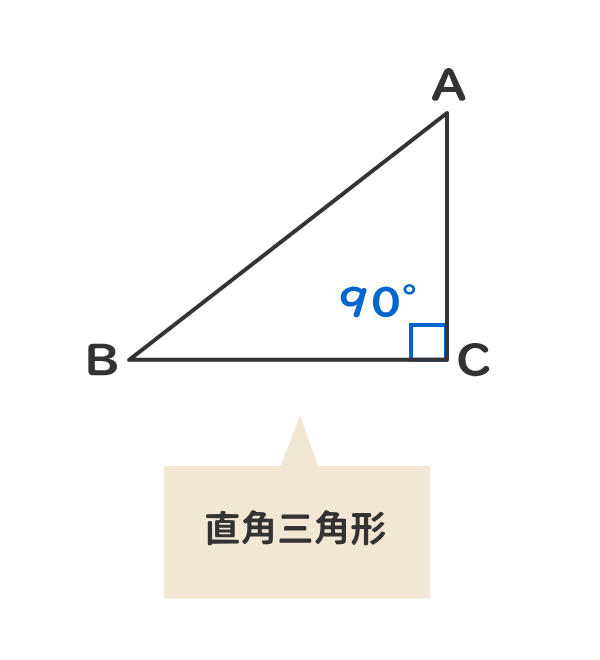



二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web



Studydoctor三角形の内角と分類 中2数学 Studydoctor



1




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
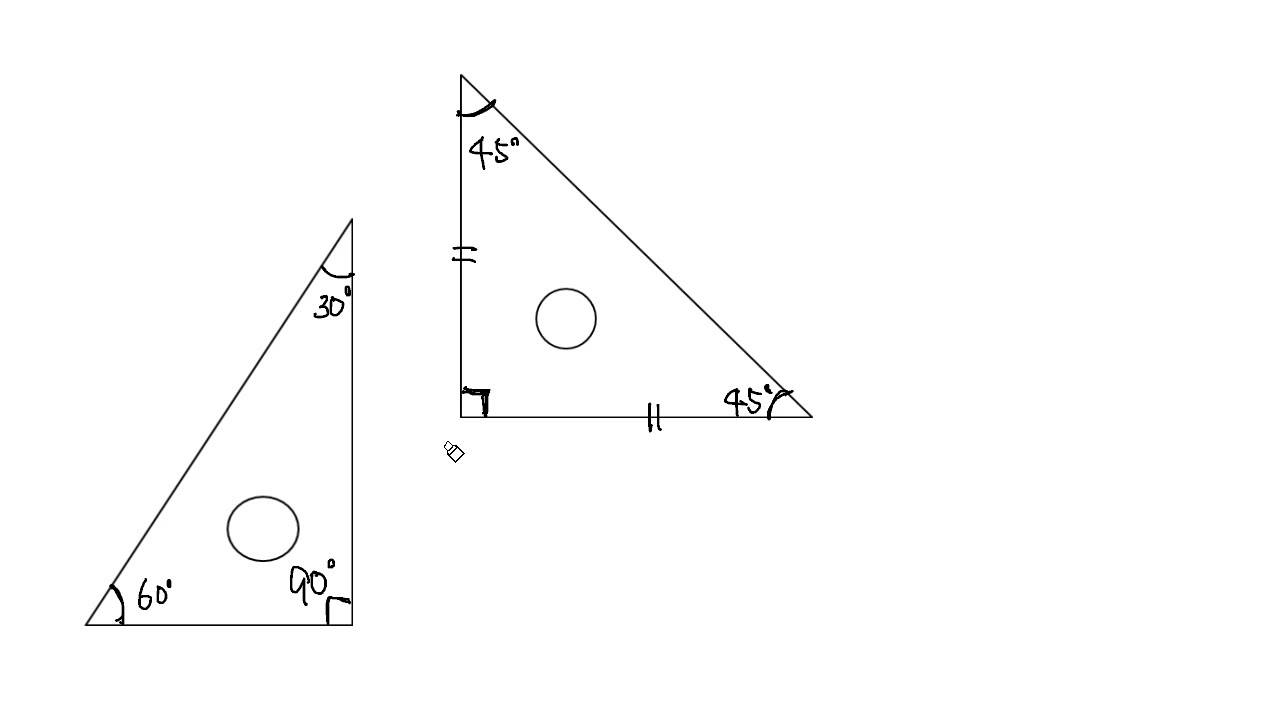



三角形の内角の和 Youtube




角度計算 みんなの知識 Apfigp
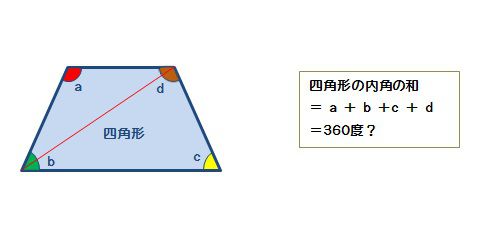



四角形の内角の和 算数の公式覚えてますか
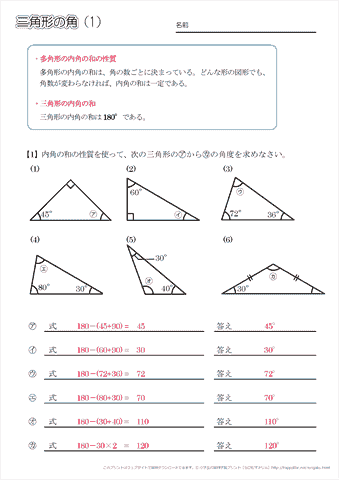



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



課題学習の指導 数学
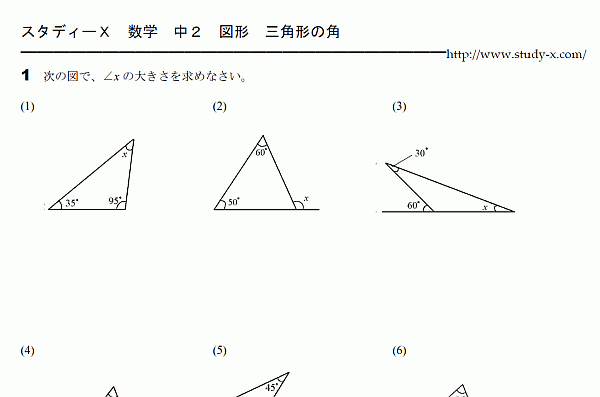



三角形の角 無料学習プリント教材
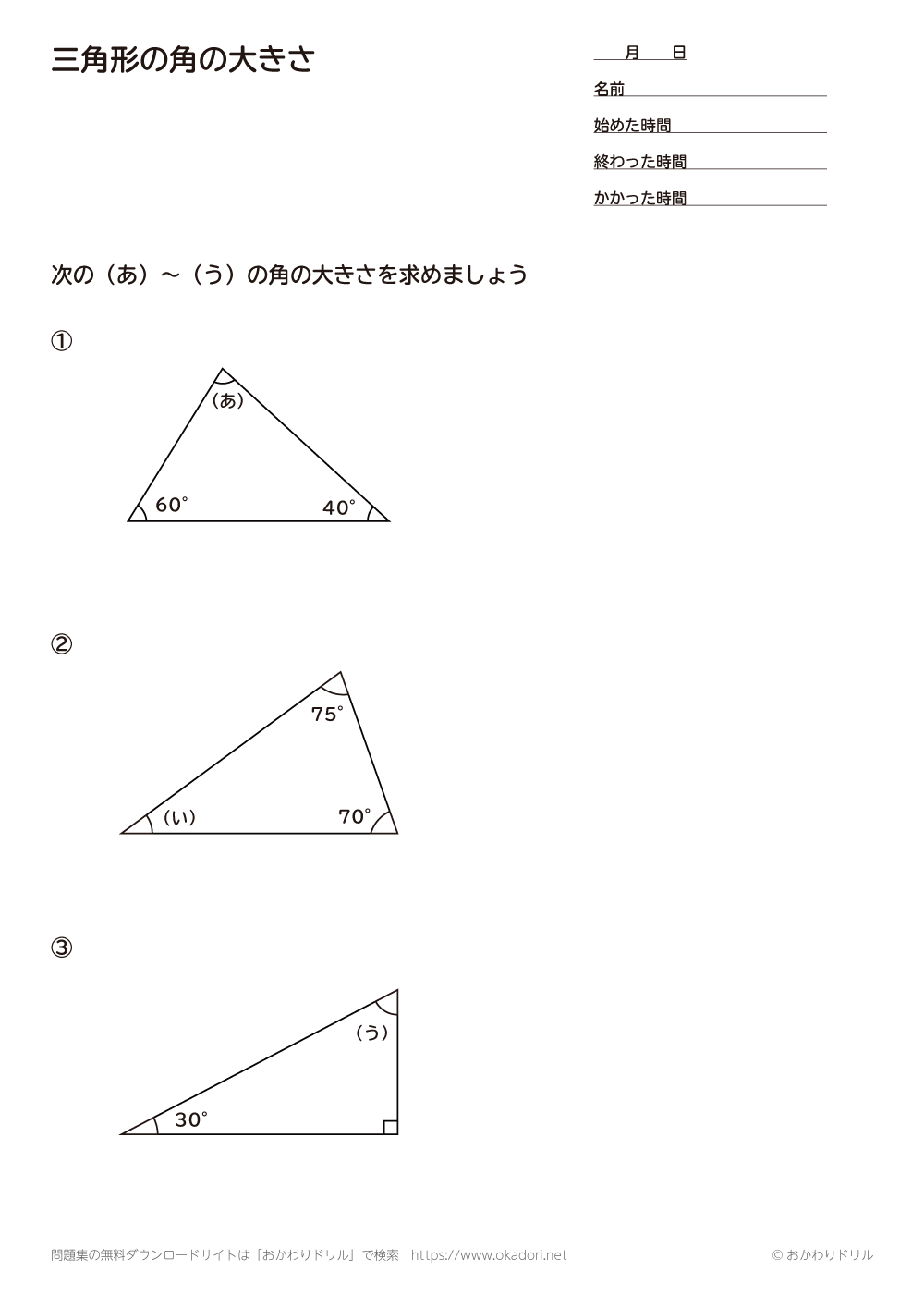



小学5年生 算数 無料問題集 三角形の角の大きさ おかわりドリル

No comments: